viernes, 4 de julio de 2008
Álgebra lineal
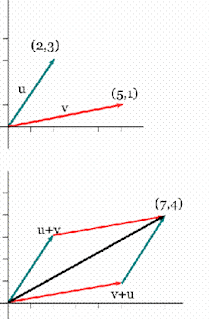
El álgebra lineal es la rama de las matemáticas que estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales, y transformaciones lineales.
Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.
La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann publicó su libro Die lineale Ausdehnungslehre.
Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.
La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann publicó su libro Die lineale Ausdehnungslehre.
ORIGEN DE LAS MATEMATICAS
ORIGEN DE LAS MATEMÁTICAS
CRONOLOGICO
HISTORICO
TEMATICO
1600 a.C.: se redacta el Papiro del Rhind, el primer texto matemático encontrado de la historia, en el antiguo Egipto.640 a.C.: nace Tales de Mileto, autor de un teorema que lleva su nombre y considerado como el inventor de la matemática deductiva.580 a.C.: nace Pitágoras, pionero de un gran movimiento metafísico moral, religioso y científico alrededor de su saber: la geometría elemental.287 a.C.: Arquímedes, el matemático más importante de la Grecia clásica, elabora teorías como el Principio de la Palanca.1202: Leonardo Pisano Fibonacci publica Liber abaci, obra que recupera los estudios de teóricos clásicos
CRONOLOGICO
HISTORICO
TEMATICO
1600 a.C.: se redacta el Papiro del Rhind, el primer texto matemático encontrado de la historia, en el antiguo Egipto.640 a.C.: nace Tales de Mileto, autor de un teorema que lleva su nombre y considerado como el inventor de la matemática deductiva.580 a.C.: nace Pitágoras, pionero de un gran movimiento metafísico moral, religioso y científico alrededor de su saber: la geometría elemental.287 a.C.: Arquímedes, el matemático más importante de la Grecia clásica, elabora teorías como el Principio de la Palanca.1202: Leonardo Pisano Fibonacci publica Liber abaci, obra que recupera los estudios de teóricos clásicos
IMPORTANCIA DE LAS MATEMATICAS
IMPORTANCIA DE LAS MATEMÁTICAS
Parece natural que la mayoría de la población desconozca casi todo sobre las matemáticas y que su relación con ellas se limite a las cuatro reglas. Este distanciamiento contrasta con la importancia que las matemáticas tienen hoy en la sociedad.
Las matemáticas están en el centro de nuestra cultura y su historia se confunde, a menudo, con la de la filosofía.
Parece natural que la mayoría de la población desconozca casi todo sobre las matemáticas y que su relación con ellas se limite a las cuatro reglas. Este distanciamiento contrasta con la importancia que las matemáticas tienen hoy en la sociedad.
Las matemáticas están en el centro de nuestra cultura y su historia se confunde, a menudo, con la de la filosofía.
EVOLUCION DE LAS MATEMATICAS
EVOLUCIÓN DE LAS MATEMÁTICAS
Enunciados de un problema matemático.
La reforma de la enseñanza nos interesa a todos. Un grupo de docentes ha examinado la cuestión del enunciado de un problema.
Plan de 1960: Un campesino vende un saco de patatas por 1000 pesetas. Los gastos de producción se elevan a 4/5 partes del precio de venta, ¿Qué beneficio obtiene? Enseñanza tradicional 1970: Un campesino vende un saco de patatas por 1OOO pesetas. Los gastos de producción se elevan a 4/5 partes del precio de venta, es decir, a 800 pesetas. ¿Que beneficio obtiene?
Enseñanza moderna 1970: Un campesino establece una correspondencia F entre un conjunto P de patatas y un Conjunto M de monedas. El cardinal del conjunto M es igual a 1000 y cada elemento PFM vale una peseta. Dibuja 1000 puntos gordos que representen los elementos del conjunto M. El conjunto G de los gastos de producción contiene 200 elementos menos que el conjunto M. Da respuesta a la pregunta siguiente: ¿Cuál es el cardinal del conjunto B de los beneficios? (Dibuja este conjunto en rojo)
Enseñanza renovada 1980: Un agricultor vende un saco de patatas por 1000 pesetas. Los gastos de producción se elevan a 800 pesetas y el beneficio es de 200 pesetas. Tarea: subraya la palabra "patatas" y discútela con tu compañero.
Enseñanza reformada, 1980: Un payes kapitalista privilejiao s`anrequesio injustamente de 200 pelas con una tocha d\`patata, analisa el testo y busca Ias fartas d\´ortografía, de sintáis y de puntuación y cuenta de que tu piensas de su manera de s\`enriquesé.
Enseñanza asistida por ordenador, 1990 Un productor del espacio agrícola en red de área global peticiona un data-bank conversacional que le displaya el day-rate de la patata. Después se baja un software computacional fiable y determina el cash-flow sobre pantalla de mapa de bits (bajo MS-D0S, configuración floppy y disco duro de 40 megabytes) Dibuja con el ratón el contorno integrado 3D del saco de patatas. Después haces un log-in a la Red por 36.15 código BP (Blue Potatoe) y sigues las indicaciones del menú.
Enunciados de un problema matemático.
La reforma de la enseñanza nos interesa a todos. Un grupo de docentes ha examinado la cuestión del enunciado de un problema.
Plan de 1960: Un campesino vende un saco de patatas por 1000 pesetas. Los gastos de producción se elevan a 4/5 partes del precio de venta, ¿Qué beneficio obtiene? Enseñanza tradicional 1970: Un campesino vende un saco de patatas por 1OOO pesetas. Los gastos de producción se elevan a 4/5 partes del precio de venta, es decir, a 800 pesetas. ¿Que beneficio obtiene?
Enseñanza moderna 1970: Un campesino establece una correspondencia F entre un conjunto P de patatas y un Conjunto M de monedas. El cardinal del conjunto M es igual a 1000 y cada elemento PFM vale una peseta. Dibuja 1000 puntos gordos que representen los elementos del conjunto M. El conjunto G de los gastos de producción contiene 200 elementos menos que el conjunto M. Da respuesta a la pregunta siguiente: ¿Cuál es el cardinal del conjunto B de los beneficios? (Dibuja este conjunto en rojo)
Enseñanza renovada 1980: Un agricultor vende un saco de patatas por 1000 pesetas. Los gastos de producción se elevan a 800 pesetas y el beneficio es de 200 pesetas. Tarea: subraya la palabra "patatas" y discútela con tu compañero.
Enseñanza reformada, 1980: Un payes kapitalista privilejiao s`anrequesio injustamente de 200 pelas con una tocha d\`patata, analisa el testo y busca Ias fartas d\´ortografía, de sintáis y de puntuación y cuenta de que tu piensas de su manera de s\`enriquesé.
Enseñanza asistida por ordenador, 1990 Un productor del espacio agrícola en red de área global peticiona un data-bank conversacional que le displaya el day-rate de la patata. Después se baja un software computacional fiable y determina el cash-flow sobre pantalla de mapa de bits (bajo MS-D0S, configuración floppy y disco duro de 40 megabytes) Dibuja con el ratón el contorno integrado 3D del saco de patatas. Después haces un log-in a la Red por 36.15 código BP (Blue Potatoe) y sigues las indicaciones del menú.
PLANO CARTESIANO
EL PLANO CARTESIANO
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.
Las coordenadas se forman asociando un valor del eje de las ‘X’ y uno de las ‘Y’, respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se representa como:
P (x, y)
Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.
Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano.
Este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano.
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.
Las coordenadas se forman asociando un valor del eje de las ‘X’ y uno de las ‘Y’, respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se representa como:
P (x, y)
Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.
Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano.
Este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano.
M.C.D. POLINOMIOS
M.C.D. DE POLINOMIOS
Al hallar el M.C.D. de dos o más polinomios puede ocurrir que los polinomios puedan facturarse fácilmente o que su descomposición no sea sencilla. En el primer caso se halla el M.C.D. por divisiones sucesivas
M.C.D. DE PLONOMIOS POR DESCOMPOSICIÓN EN FACTORES
REGLA
Se descomponen los polinomios dados en sus factores primos. El M.C.D. es el producto de los factores comunes con su menor exponente.
Ejemplos
(1)
FACTORANDO ESTAS EXPRESIONESSSS:Hallar el M.C.D. de 4a² + 4ab y 2a⁴ = 2a²b².
4a² + 4ab = 4a(a + b) = 2²a(a + b)
2a⁴ - 2a²b² = (a² - b²) = 2a²(a + b) (a - b)
Los factores comunes son 2, a y (a + b). R.
M.C.D. = 2ª (a + b).
(2) Hallar el M.C.D. de x² - 4, x² - x – 6 y x² + 4x + 4
FACTORANDOX² - 4 =(x + 2)(x – 2)
X² - x – 6=(x – 3)(x + 2)
X² + 4x + 4=(x – 2)²
El factor común es (x + 2) y se toma con su menor exponente, luego:
M.C.D. = x + 2
Al hallar el M.C.D. de dos o más polinomios puede ocurrir que los polinomios puedan facturarse fácilmente o que su descomposición no sea sencilla. En el primer caso se halla el M.C.D. por divisiones sucesivas
M.C.D. DE PLONOMIOS POR DESCOMPOSICIÓN EN FACTORES
REGLA
Se descomponen los polinomios dados en sus factores primos. El M.C.D. es el producto de los factores comunes con su menor exponente.
Ejemplos
(1)
FACTORANDO ESTAS EXPRESIONESSSS:Hallar el M.C.D. de 4a² + 4ab y 2a⁴ = 2a²b².
4a² + 4ab = 4a(a + b) = 2²a(a + b)
2a⁴ - 2a²b² = (a² - b²) = 2a²(a + b) (a - b)
Los factores comunes son 2, a y (a + b). R.
M.C.D. = 2ª (a + b).
(2) Hallar el M.C.D. de x² - 4, x² - x – 6 y x² + 4x + 4
FACTORANDOX² - 4 =(x + 2)(x – 2)
X² - x – 6=(x – 3)(x + 2)
X² + 4x + 4=(x – 2)²
El factor común es (x + 2) y se toma con su menor exponente, luego:
M.C.D. = x + 2
martes, 1 de julio de 2008
las matemáticas
Las matemáticas son el estudio de las relaciones entre cantidades, magnitudes y propiedades, y de las operaciones lógicas utilizadas para deducir cantidades, magnitudes y propiedades desconocidas. Las matemáticas son tan antiguas como la propia humanidad.
la gráfica
La función a la que me refiero es muy sencilla, se trata simplemente de la función inversa de x, es decir, de
y= 1 / x
cuya gráfica es la siguiente:
Pues bien, Torricelli descubrió en 1643 que el sólido de revolución generado al rotar esta curva alrededor del eje x desde x=1 hasta x=¥ tiene volumen finito. Esto causó una auténtica sorpresa en su tiempo y el filósofo inglés Thomas Hobbes llegó a decir en 1672:
"Para entender este sin sentido no hace falta que una persona sea lógico o geómetra, sino que esté loco"
y= 1 / x
cuya gráfica es la siguiente:
Pues bien, Torricelli descubrió en 1643 que el sólido de revolución generado al rotar esta curva alrededor del eje x desde x=1 hasta x=¥ tiene volumen finito. Esto causó una auténtica sorpresa en su tiempo y el filósofo inglés Thomas Hobbes llegó a decir en 1672:
"Para entender este sin sentido no hace falta que una persona sea lógico o geómetra, sino que esté loco"
¿saben matemáticas las abejas

Puede parecer una pregunta tonta, pero ¿saben matemáticas las abejas?.Este hecho ya fue constatado por Papus de Alejandría, matemático griego que vivió del año 284 al 305.
Su afirmación se basaba en la forma hexagonal que imprimen a sus celdillas las abejas para guardar la miel.
Las abejas, cuando guardan la miel, tienen que resolver varios problemas. Necesitan guardar la miel en celdillas individuales, de tal manera que formen un mosaico sin huecos ni salientes entre las celdillas, ya que hay que aprovechar el espacio al máximo.
Solo podrían hacerlo con triángulos, cuadrados y hexágonos. ¿Por que eligieron entonces los hexágonos, si son mas difícil de construir?.
La respuesta es un problema isoperimétrico (del griego "igual perímetro"). Papus había demostrado que, entre todos los polígonos regulares con el mismo perímetro, encierran mas área aquellos que tengan mayor número de lados. Por eso, la figura que encierra mayor área para un perímetro determinado es el círculo, que posee un número infinito de lados.
Por eso las abejas construyen sus celdillas de forma hexagonal, ya que, gastando la misma cantidad de cera en las celdillas, consiguen mayor superficie para guardar su miel.
La pregunta es: ¿y quien le enseñó esto a las abejas?....
Su afirmación se basaba en la forma hexagonal que imprimen a sus celdillas las abejas para guardar la miel.
Las abejas, cuando guardan la miel, tienen que resolver varios problemas. Necesitan guardar la miel en celdillas individuales, de tal manera que formen un mosaico sin huecos ni salientes entre las celdillas, ya que hay que aprovechar el espacio al máximo.
Solo podrían hacerlo con triángulos, cuadrados y hexágonos. ¿Por que eligieron entonces los hexágonos, si son mas difícil de construir?.
La respuesta es un problema isoperimétrico (del griego "igual perímetro"). Papus había demostrado que, entre todos los polígonos regulares con el mismo perímetro, encierran mas área aquellos que tengan mayor número de lados. Por eso, la figura que encierra mayor área para un perímetro determinado es el círculo, que posee un número infinito de lados.
Por eso las abejas construyen sus celdillas de forma hexagonal, ya que, gastando la misma cantidad de cera en las celdillas, consiguen mayor superficie para guardar su miel.
La pregunta es: ¿y quien le enseñó esto a las abejas?....
El truco es el siguiente: Pedís a alguien que os escriba un número de cuatro cifras. En un papel aparte restáis 2 a esa cifra y le ponéis un 2 delante:
Ejemplo: Si escriben 2435 vosotros escribiréis 22433
Escribís el número aparte, sin que nadie os vea. Después pedís a alguien que escriba otro número de 4 cifras debajo. Una vez hecho esto, decís que el siguiente lo vais a escribir vosotros. Tenéis que completar con nueves (es decir, hacer que la suma de vuestra cifra y la anterior de todo nueves).
Ejemplo: Si el primer número que han puesto es el 2435 y el segundo el 2354
243523547645
Hemos puesto el 7645 porque 7+2=9, 6+3=9, 5+4=9 y 4+5=9. Tenéis que ponerlo simulando que lo ponéis al azar.
Una vez hecho esto, repetimos la operación otra vez, decimos que pongan otro número de cuatro cifras debajo, y nosotros volvemos a poner otro completando a nueves con el anterior
24352354764542785721
Ahora viene lo bueno: decimos a alguien que sume toda la columna. El resultado será el número que previamente habíamos copiado en un papel. Consejo: verificar antes porque casi todo el mundo se equivoca al hacer la suma.
Explicación: No tiene nada de misterioso. Fijémonos en los pares 2-3 y 4-5 de la columna. Ambos suman 9999, por lo que los 4 suman 19.998. Es decir, 20.000 menos 2. Sumado a la primer cifra es lo mismo que restarle 2 y ponerle un 2 delante.
Ejemplo: Si escriben 2435 vosotros escribiréis 22433
Escribís el número aparte, sin que nadie os vea. Después pedís a alguien que escriba otro número de 4 cifras debajo. Una vez hecho esto, decís que el siguiente lo vais a escribir vosotros. Tenéis que completar con nueves (es decir, hacer que la suma de vuestra cifra y la anterior de todo nueves).
Ejemplo: Si el primer número que han puesto es el 2435 y el segundo el 2354
243523547645
Hemos puesto el 7645 porque 7+2=9, 6+3=9, 5+4=9 y 4+5=9. Tenéis que ponerlo simulando que lo ponéis al azar.
Una vez hecho esto, repetimos la operación otra vez, decimos que pongan otro número de cuatro cifras debajo, y nosotros volvemos a poner otro completando a nueves con el anterior
24352354764542785721
Ahora viene lo bueno: decimos a alguien que sume toda la columna. El resultado será el número que previamente habíamos copiado en un papel. Consejo: verificar antes porque casi todo el mundo se equivoca al hacer la suma.
Explicación: No tiene nada de misterioso. Fijémonos en los pares 2-3 y 4-5 de la columna. Ambos suman 9999, por lo que los 4 suman 19.998. Es decir, 20.000 menos 2. Sumado a la primer cifra es lo mismo que restarle 2 y ponerle un 2 delante.
geometría analítica
Geometría analítica
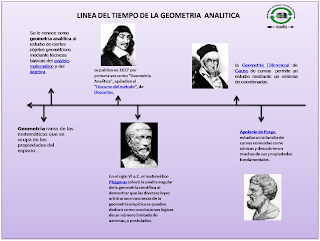
Se le conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra. Se podría decir que es el desarrollo histórico que comienza con la geometría cartesiana y concluye con la aparición de la geometría diferencial con Gauss y más tarde con el desarrollo de la geometría algebraica.
Lo novedoso de la Geometría Analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: 2x + 6y = 0) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia x2 + y2 = 4, la hipérbola xy = 1 ).
Se le conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra. Se podría decir que es el desarrollo histórico que comienza con la geometría cartesiana y concluye con la aparición de la geometría diferencial con Gauss y más tarde con el desarrollo de la geometría algebraica.
Lo novedoso de la Geometría Analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: 2x + 6y = 0) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia x2 + y2 = 4, la hipérbola xy = 1 ).
De Wikipedia, la enciclopedia libre
EL DIABLO DE LOS NUMEROS

Para Maestros
Materiales educativos, carpeta pedagógica, registros para maestros.
19/10/07
EL DIABLO DE LOS NÚMEROS
Un libro para todos aquellos que temen las matemáticas. 259 páginas. ¿Cómo hacer que a tus alumnos les gusten las matemáticas?. Este libro trata la historia de un niño que odiaba los números, pero gracias a un diablillo, logra que le encanten.
IntroducciónA Robert no le gustan las Matemáticas, como sucede a muchas personas, porque no las acaba de entender. Pero una noche él sueña con un diablillo que pretende iniciarle en la ciencia de los números. Naturalmente, Robert piensa que es otra de sus frecuentes pesadillas, pero en realidad es el comienzo de un recorrido nuevo y apasionante a través del mundo de las Matemáticas. ¿No es extraño hallar siempre secuencias numéricas por la simple multiplicación de los unos: 1 x 1 = 1 11 x 11=121 111111 x 111111 = 12345654321 y así en adelante? Y esto es sólo la operación más sencilla. Durante doce noches, Robert sueña sistemas numéricos cada vez más increíbles. De pronto, los números cobran vida por sí mismos, una vida misteriosa que ni siquiera el diablo puede explicar del todo. Nunca las Matemáticas habían sido algo tan fascinante. Pronto, el diablo le hará abandonar los tópicos escolares y hará que acceda a niveles superiores: ¡y aun así los entiende! Y el joven lector también. Los números, cada página que pasa, se van volviendo cada vez más absorbentes. Es como magia, y Robert quiere saber más y más basta que, al fin, el diablo le hace comprender que algunos problemas y paradojas pertenecen a las altas esferas de la ciencia.
Materiales educativos, carpeta pedagógica, registros para maestros.
19/10/07
EL DIABLO DE LOS NÚMEROS
Un libro para todos aquellos que temen las matemáticas. 259 páginas. ¿Cómo hacer que a tus alumnos les gusten las matemáticas?. Este libro trata la historia de un niño que odiaba los números, pero gracias a un diablillo, logra que le encanten.
IntroducciónA Robert no le gustan las Matemáticas, como sucede a muchas personas, porque no las acaba de entender. Pero una noche él sueña con un diablillo que pretende iniciarle en la ciencia de los números. Naturalmente, Robert piensa que es otra de sus frecuentes pesadillas, pero en realidad es el comienzo de un recorrido nuevo y apasionante a través del mundo de las Matemáticas. ¿No es extraño hallar siempre secuencias numéricas por la simple multiplicación de los unos: 1 x 1 = 1 11 x 11=121 111111 x 111111 = 12345654321 y así en adelante? Y esto es sólo la operación más sencilla. Durante doce noches, Robert sueña sistemas numéricos cada vez más increíbles. De pronto, los números cobran vida por sí mismos, una vida misteriosa que ni siquiera el diablo puede explicar del todo. Nunca las Matemáticas habían sido algo tan fascinante. Pronto, el diablo le hará abandonar los tópicos escolares y hará que acceda a niveles superiores: ¡y aun así los entiende! Y el joven lector también. Los números, cada página que pasa, se van volviendo cada vez más absorbentes. Es como magia, y Robert quiere saber más y más basta que, al fin, el diablo le hace comprender que algunos problemas y paradojas pertenecen a las altas esferas de la ciencia.
Suscribirse a:
Comentarios (Atom)